Febrero

LAPLACIANO DE UN CAMPO ESCALAR 

INTEGRALES DE LINEA

Es una integral cuya función se encuentra evaluada sobre una curva C. Tiene varias aplicaciones, como determinar la longitud de una curva o para determinar el trabajo realizado por una partícula. La integral de linea esta definida por la siguiente expresión:

Para la resolución de estas integrales, se debe seguir los siguientes pasos:
1. Parametrizar las variables
2. Derivar las variables parametrizadas
3. Reemplazar las nuevas variables en la función f(x,y)
4. Simplificar algebraicamente lo que sea posible
5. Resolver la integral

DEFINICIÓN

INDEPENDENCIA DE LA TRAYECTORIA

ABRIR ENLACE

TEOREMA DE GREEN 

El teorema de Green da la relación entre una integral de línea alrededor de una curva cerrada simple C y una integral doble sobre la región plana D limitada por C. El teorema de Green se llama así por el científico británico George Green, y resulta ser un caso especial del más general teorema de Stokes. El teorema afirma:

Sea C una curva cerrada simple positivamente orientada, diferenciable por trozos, en el plano y sea D la región limitada por C. Si P y Q tienen derivadas parciales continuas en una región abierta que contiene D,

${\displaystyle \int _{C^{+}}(P\,dx+Q\,dy)=\int \!\!\!\int _{D}\left({\frac {\partial Q}{\partial x}}-{\frac {\partial P}{\partial y}}\right)\,dA}$

A veces la notación

${\displaystyle \oint _{C^{+}}(P\,dx+Q\,dy)}$

se utiliza para establecer que la integral de línea está calculada usando la orientación positiva (antihoraria) de la curva cerrada C.

ROTACIONAL

En el cálculo vectorial, el rotacional o rotor es un operador vectorial sobre campos vectoriales definidos en un abierto de ${\displaystyle \mathbb {R} ^{3}}$ que muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto.

Matemáticamente, esta idea se expresa como el límite de la circulación del campo vectorial, cuando la curva sobre la que se integra se reduce a un punto:

${\displaystyle \mathbf {U} \cdot {\mbox{rot}}\ \mathbf {F} =\mathbf {U} \cdot \nabla \times \mathbf {F} \equiv \lim _{\Delta S\to 0}{\frac {1}{\Delta S}}\oint _{C}\mathbf {F} \cdot {\text{d}}\mathbf {r} }$

Aquí, ${\displaystyle \Delta S}$ es el área de la superficie apoyada en la curva ${\displaystyle C}$, que se reduce a un punto. El resultado de este límite no es el rotacional completo (que es un vector), sino solo su componente según la dirección normal a ${\displaystyle \Delta S}$ y orientada según la regla de la mano derecha. Para obtener el rotacional completo deberán calcularse tres límites, considerando tres curvas situadas en planos perpendiculares.

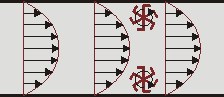
Aunque el que el rotacional de un campo alrededor de un punto sea distinto de cero no implica que las líneas de campo giren alrededor de ese punto y lo encierren. Por ejemplo, el campo de velocidades de un fluido que circula por una tubería (conocido como perfil de Poiseuille) posee un rotacional no nulo en todas partes, salvo en el eje central, pese a que la corriente fluye en línea recta:

La idea es que si colocamos una rueda de paletas infinitamente pequeña en el interior del campo vectorial, esta rueda girará, aunque el campo tenga siempre la misma dirección, debido a la diferente magnitud del campo a un lado y a otro de la rueda.

DIVERGENCIA

La divergencia de un campo vectorial 

en coordenadas rectangulares se define como el producto escalar del operador nabla por la función

La divergencia es una función escalar del campo vectorial. El teorema de la divergencia es una herramienta matemática importante en la Electricidad y el Magnetismo. 

Aplicaciones de Divergencia

Divergencia. Varias Coordendas

Comparada con la divergencia en coordenadas rectangulares:
En coordenadas polar cilíndrica:
y en coordenadas polar esférica:

ENLACE DEL TEOREMA DE DIVERGENCIA VIDEO