CLASE N°1
11-10-2016
Fue el primer día de clases, donde se presento la Ing. Mónica Maltilla quien impartira la cátedra de calculo vectorial. se realizo una breve introducción de lo que se verá en el semestre ademas se trato de diferentes normas y parámetros para el desarrollo de las clases como:
VALORES
Este parámetro es muy importante ya que con ellos podemos tener un ambiente mas apropiado para estudiar, entre los valores que se destacan son:
- Puntualidad
- Respeto
- Honestidad
CLASE N°2
14-10-2016
Vectores y Geometría Analítica en el Espacio
Funciones Implícitas de dos variables
En F(x, y) = 0
F(x, y) = 0
Existen 2 funciones:
y=f(x) ; y=f2(x)
x=g(y) ; x=g2(y)
Generalmente estas funciones, representan una curva en el plano .
.
Ejemplo:
x^2+y^2-9=0 Circulo
En
 F(x, y) = 0
F(x, y) = 0Existen 2 funciones:
y=f(x) ; y=f2(x)
x=g(y) ; x=g2(y)
Generalmente estas funciones, representan una curva en el plano
 .
.Ejemplo:
x^2+y^2-9=0 Circulo

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEg44uH3BXYTSL4DpTSxJiLmqi7v_UjSSfqdzPxm0-1TQ88gWbhNobFZTjvq2wsKQc6bPp1Njh3EH8vP0XokRD_QRCeIUZxDsE55JaceIMDIP-AUDp4F0u4rNimhjf0JCz0ZYfnpCdsS2bg/s1600/circle.gif
Funciones Implícitas en el Espacio
En el espacio R3 Las funciones implícitas representan una superficie en el espacio F(x,y,z)=0 .
Por ejemplo:
x^2+y^2+z^2 = r^2 Ecuación de una superficie esférica de centro (0,0,0) y radio = r.
 http://enciclopedia.us.es/images/b/b5/Elipsoide_de_revoluci%C3%B3n_canto_rodado.png
http://enciclopedia.us.es/images/b/b5/Elipsoide_de_revoluci%C3%B3n_canto_rodado.png
CLASE N°3
25-10-2016
Ecuaciones de la Recta en el Espacio
x^2+y^2+z^2 = r^2 Ecuación de una superficie esférica de centro (0,0,0) y radio = r.

http://enciclopedia.us.es/images/b/b5/Elipsoide_de_revoluci%C3%B3n_canto_rodado.png
25-10-2016
Ecuaciones de la Recta en el Espacio
Una recta en el espacio queda determinada por un punto de ella A ( x1, y1, z1) y un vector director u→ = ( a, b, c)
Ecuaciones de la recta

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEggB8lQw0s_vBRAvAXBk2O4cVW5ur14MG81ejIlC2-p8MwaG7Xyhbm89Sp69CQGMQnF4LfXEefl9ioujebvjySYC8Od9vaQbtEPZkbThmoZ0tugSWdH1EaENzyuBAHD5ViDg0IpMpokk7IO/s1600/rectas-1.gif
Referencia:Libro Cálculo de Varias Variables de Stewart.
Ecuaciones del Plano en el Espacio

https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgFjlSeaklA_1DZljWpqy-vNKKdoZ6JUH2neKb8CEu7t0JBJuTvm00qc3RSRYFMgH_LRvfzaQPq0s7TayKWdOYEr17tyjgV-_CknQKZKFAUOukc0vzoSG87Cpn7vs7mNTLRw9FobPvZHdio/s400/slide_9.jpg
ECUACIÓN SEGMENTARÍA DEL PLANO
Ax+By+Cz+D=0
Ax+By+Cz=-D
x/-(D/A)+x/-(D/B)+x/-(D/C)=1
a=-(D/A)
b=-(D/B)
c=-(D/C)
==> x/a + y/b +z/c =1 Ecuación Segmentaria del plano
https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhbRPZle9nhzzqTLJTclqbeACn4IK5EGmmeSSFWaOr_mQFOEkexdg1ZLrrB9pU7B0pfXfyulQY6WgiilAvKAZ9ygwth-xSUpbPNLvbAxg7lQE-9qkLdYJ2ptYi7F1XoVzgcev1WL3kl17Ky/s1600/segm.bmp
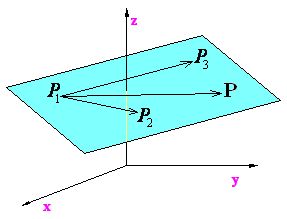
ECUACIÓN PLANO DADO TRES PUNTOS

http://www.aulafacil.com/uploads/cursos/748/editor/planoenelespacio89.jpg
Datos:
M1=r1=(x1,y1,z1)
M2=r2=(x2,y2,z2)
M3=r3=(x3,y3,z3)
Dados estos datos la ecuación vectorial entre tres puntos es:
(r-r1)•(r2-r1)x(r3-r1)=0 Ecuación del Plano dados tres puntos(producto mixto)
El producto mixto (o también conocido como triple producto escalar) es una operación entre tres vectores que combina el producto escalar con el producto vectorial para obtener un resultado un escalar.
*Si el producto mixto es igual a cero, entonces los tres vectores son COPLANARES.
*El producto mixto generalmente representa el volumen del paralelepípedo cuyas aristas son los tres vectores.
* EL VOLUMEN: C.(AxB) u^3
EL ANGULO ENTRE DOS PLANOS
CLASE N°4
28-10-2016
DISTANCIA DE UN PUNTO A UN PLANO
La distancia de un punto, P, a un plano, π, es la menor de la distancia desde el punto a los infinitos puntos del plano. Esta distancia corresponde a la perpendicular trazada desde el punto al plano.










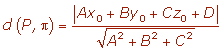

No hay comentarios:
Publicar un comentario